
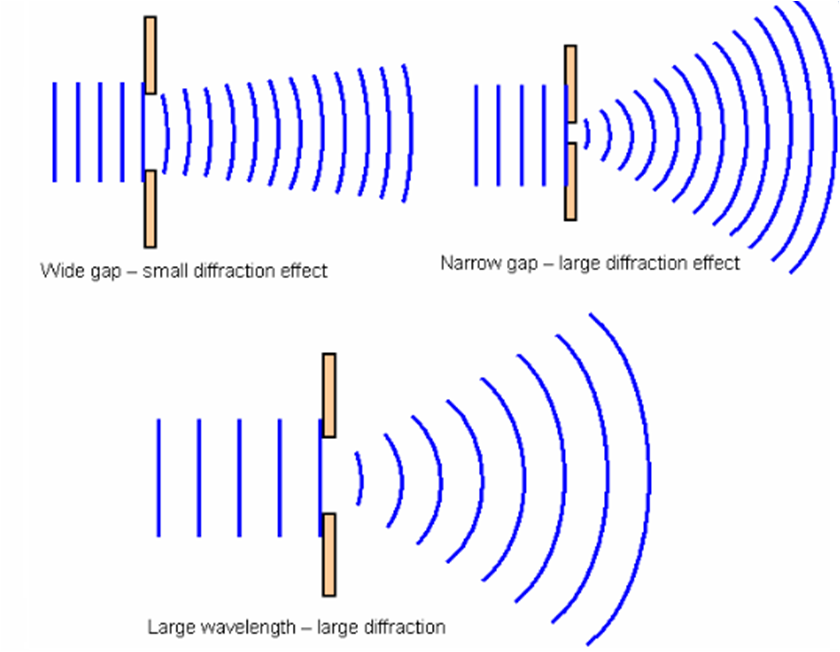
In all cases we analyze the possibilities of various approximations which can be made, and show the limits and validity of the Fraunhofer approximation both in space and in time. Then we analyze in detail diffraction at an edge, both in space and in time, of a single slit in space and in time, a double slit in space, and a single slit in time, a single slit in space and a double slit in time, and, finally, a double slit both in space and in time. We then investigate in detail the simultaneous diffraction both in space and in time representing a general solution. Specific cases of diffraction in time investigated here are diffraction at an “edge in time” and a Fresnel lens in time. The propagation of a wave can be visualized by considering every particle of the transmitted medium on a wavefront as a point source for a secondary spherical wave. Diffraction in time appears for Schrödinger waves and not for light in vacuum. In classical physics diffraction arises because of the way in which waves propagate this is described by the HuygensFresnel principle and the principle of superposition of waves. It occurs when the size of the aperture or obstacle is of the.

In the present paper we investigate this phenomenon starting from a Green’s-function approach. Diffraction is the spreading out of waves as they pass through an aperture or around objects. When a wave passes through a gap or travels around an obstacle, it spreads out. In analogy to the well-known diffraction of waves at spatial structures, one can also define diffraction in time when a wave is temporarily modulated. Diffraction is a phenomena unique to waves.


 0 kommentar(er)
0 kommentar(er)
